练习三:用下方公式计算出π的近似值,直到发现某一项的绝对值小于10^-6为止(此项不计累加)。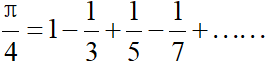
分析:
1.观察右边式子规律,把“1”看做“1/1”发现分子都是“1”而分母却是每一项之间的差距都为“2”,那么我们直到分母的规律“n=n+2”.
2.既然是求近似值,且一直按照这个式子进行计算,那么我们不可能一个一个的写出来每一项的数值,所以这里要运用到循环结构.
3.由分析“1”可知分母的规律,这样有利于循环的抒写,但我们发现这式子是每项的符号不同,+-+-+……,那么我们需要控制每次循环时,循环体的正负情况.
4.我们还要确定一下“int”的取值范围是否足够,因为我们最终要循环到“10^-6”,这里解释一下为什么是“10^-6”,因为,我们可以自行调试一下,定一个“double”类型的,并且向后输出多个位数,发现会出现几个意外的数值,因为浮点数储存时,储存的是近似值,所以我们在计算机内,我们默认的“0”就是近似于“10^-6”,我们要表示“10^-6”总不能这样表示吧“1/1000000”,感觉有点长,所以对于这种“科学计数法”我们有独特的表示方法,
就是:“1ex”
例如:
“10^-6”⇔“1e-6”
“10^6”⇔“1e6”
分析完之后,我们来写代码,
代码如下:
#include<stdio.h>
int main()
{
double n=1,sign=1,pi;
while((1/n)>=1e-6)
{
pi=pi+sign*(1/n);
n=n+2;
sign=-sign;
}
printf("π的近似值为:%f\n",pi*4);
return 0;
}
代码调试截图: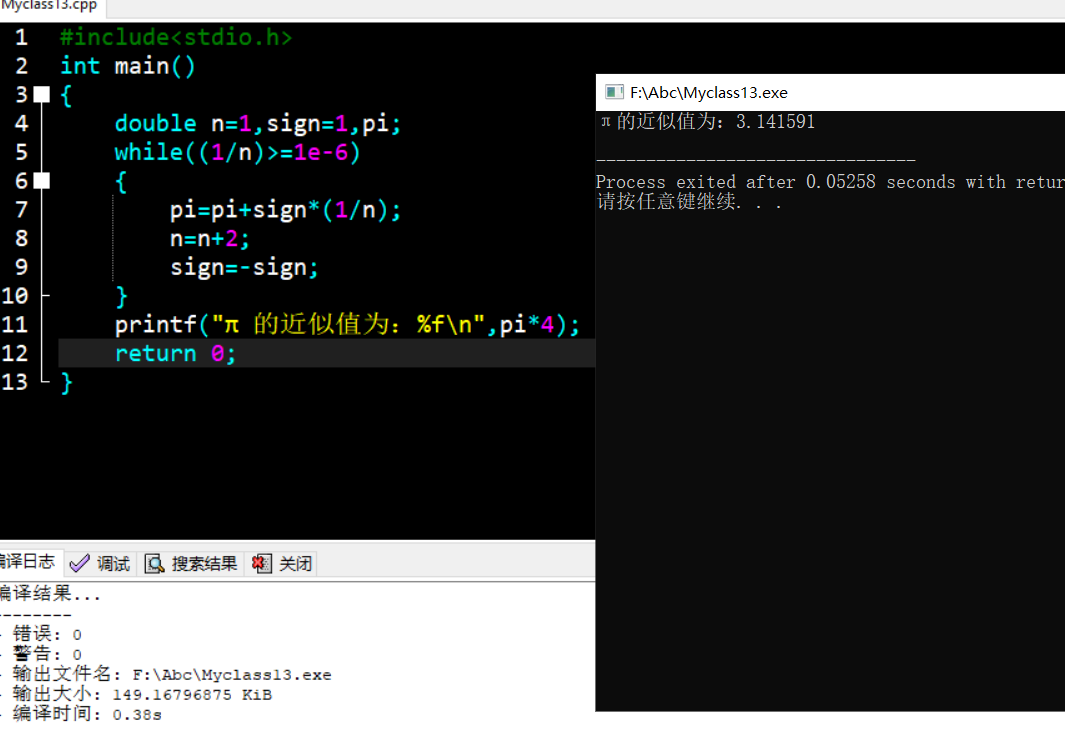
我们来看看这个程序的循环体运行了多少次,
代码如下:这里用到了“类型强制转换”因为在C语言中,“int”类型的级别比较低,而“double”类型比较高,所以我们要从级别低的向级别高的去转换,就必须使用“类型强制转换符”
#include<stdio.h>
int main()
{
double n=1,sign=1,pi,i=0;
while((1/n)>=1e-6)
{
pi=pi+sign*(1/n);
n=n+2;
sign=-sign;
i++;
}
printf("π的近似值为:%f\n运行了%d次!\n",pi*4,(int)i);
return 0;
}
代码调试截图:程序运行了50w次,,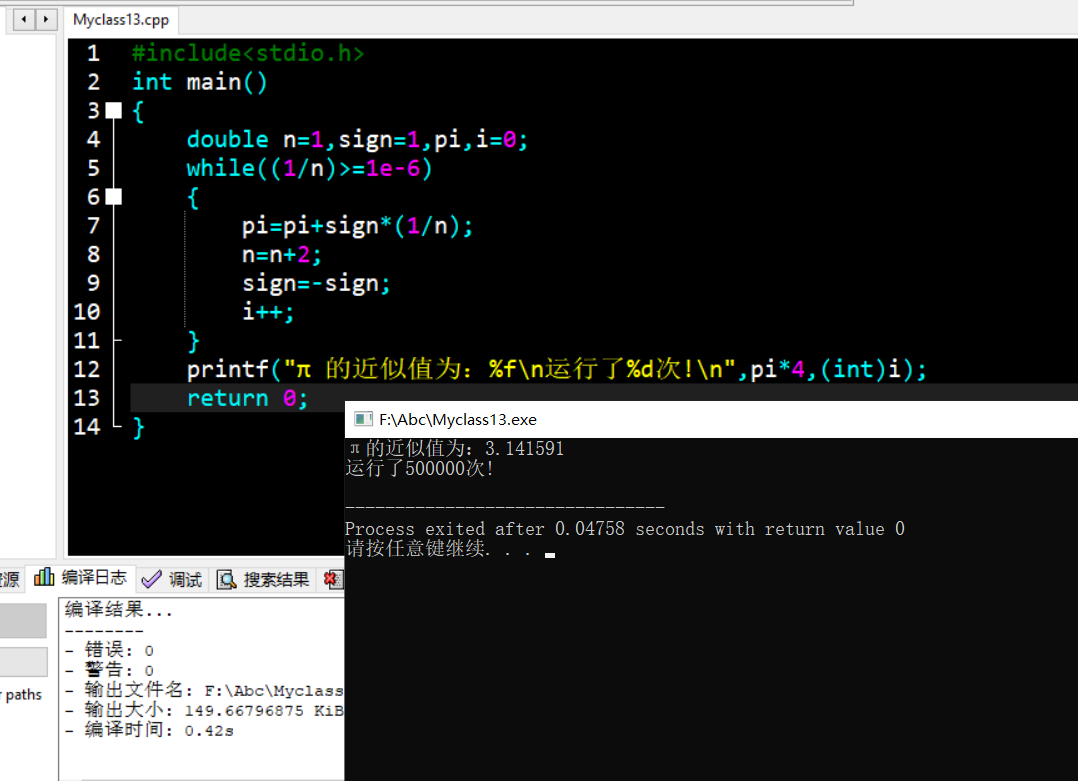
未经授权不得转载,转载时请注明出处。

评论(0)